皆さんこんにちは!ペンギンの管理人です!
猛烈に寿司打のスコアを上げていきたいと思っている今日この頃です!
ということで今回は,タイピングゲーム“寿司打”を徹底解剖していき,スコアを上げるためにはどうすれば良いのかを理論的に考えていきます!
入力反応時間について
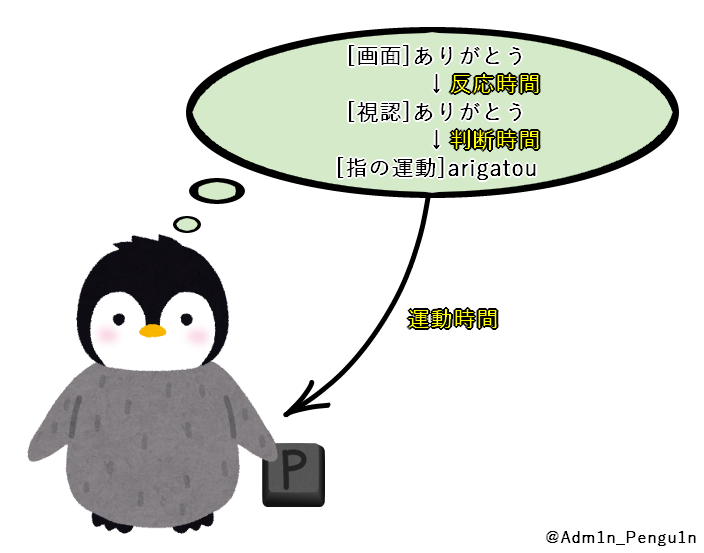
この寿司打というゲームは,“次の文章が予め表示されない”かつ“入力不能時間がない”ため,画面に表示された文字をいかに素早く打つかの能力が必要となります.
以下,その時間を入力反応時間\(T_{\rm{in}}\)と呼ぶことにします.
次に,入力反応時間\(T_{\rm{in}}\)は以下の3つの要素に分けられると考えます.
- 反応時間\(T_{\rm{r}}\)(文字を認知して指の筋肉を動かすまでにかかる時間)
- 判断時間\(T_{\rm{j}}\)(文章を認知して指をどのように動かすか判断するまでにかかる時間)
- 運動時間\(T_{\rm{m}}\)(指を指定キーの位置に移動させるまでにかかる時間)
一般的な反応時間\(T_{\rm{r}}\)は文献によってまちまちですが,反応速度テストのような単純な場合は150~300ms程度です.
また,判断時間\(T_{\rm{j}}\)や運動時間\(T_{\rm{m}}\)は“個人差”や“タイピングの熟練度”によって差が大きいと考えられます.
反応時間\(T_{\rm{r}}\)を訓練によって鍛えることは難しいですが,判断時間\(T_{\rm{j}}\)や運動時間\(T_{\rm{m}}\)はタイピングを練習すればするほど鍛えられていくはずです.
ここで,入力反応時間\(T_{\rm{in}}\)は以上の3つの要素の和として,
\begin{equation} T_{\rm{in}} = T_{\rm{r}} + T_{\rm{j}} + T_{\rm{m}}\end{equation}
と表されるとします.

入力反応時間を縮めるために、タイピングの練習を続けていきたいペン!
タイピング速度と正確性の関係について
ここでは,タイピング速度(1秒間あたりの平均タイプ数)と正確性について考えていきましょう.
このゲームには正確にタイプし続けると,画面上側のメーターが上がっていき,ある既定の位置に達すると左から順に1秒(+28keys連続),1秒(+31keys連続),2秒(+34keys連続),3秒(+36keys連続)が残り時間に加算されるという仕組みがあります.
開始の制限時間は120秒であり,総タイプ数を\(x\rm{[key]}\)とします.したがって,正味の制限時間の最大値\(T_\rm{max}\rm{[s]}\)は,
\begin{eqnarray} T_\rm{max} &=& 120 + \left\lfloor \frac{\it{x}\rm{+31+34+36}}{28+31+34+36} \right\rfloor + \left\lfloor \frac{\it{x}\rm{+34+36}}{28+31+34+36} \right\rfloor + 2\left\lfloor \frac{\it{x}\rm{+36}}{28+31+34+36} \right\rfloor + 3\left\lfloor \frac{\it{x}}{28+31+34+36} \right\rfloor \\ &=& 120 + \left\lfloor \frac{\it{x}\rm{+101}}{129} \right\rfloor + \left\lfloor \frac{\it{x}\rm{+70}}{129} \right\rfloor + 2\left\lfloor \frac{\it{x}\rm{+36}}{129} \right\rfloor + 3\left\lfloor \frac{\it{x}}{129} \right\rfloor \rm{[s]}\cdots(1) \end{eqnarray}
と表されます.ただし,\(\lfloor x \rfloor\)は\(x\)を超えない最大の整数を返す関数です(床関数).また,総タイプ数\(x\rm{[key]}\)と皿の枚数の合計\(n\)との関係は,寿司打の動画より,
\[ \frac{x}{n} = \frac{1181}{6+35+18} = 20.0… \cdots(2)\]
すなわち,\(n \simeq \frac{x}{20}\)であることがわかります.
以上より,総タイプ数\(x\rm{[key]}\)と正確性重視のタイピング速度\(V\rm{[key/s]}\)の関係は(1)式,(2)式より,
\begin{eqnarray} V &=& \frac{x}{\it{T}_\rm{max} – \it{nT}_\rm{in}} \\ &=& \simeq \frac{x}{ 120 + \left\lfloor \frac{\it{x}\rm{+101}}{129} \right\rfloor + \left\lfloor \frac{\it{x}\rm{+70}}{129} \right\rfloor + 2\left\lfloor \frac{\it{x}\rm{+36}}{129} \right\rfloor + 3\left\lfloor \frac{\it{x}}{129} \right\rfloor – \frac{(T_{\rm{r}} + T_{\rm{j}} + T_{\rm{m}}) \it{x}}{20}} \rm{[key/s]}\cdots(3)\end{eqnarray}
となります.
同様に,正味の制限時間の最小値\(T_\rm{min}\rm{[s]}\)は,
\[ T_\rm{min} = 120 \rm{[s]} \cdots(4) \]
と表され,総タイプ数\(x\rm{[key]}\)と速度重視のタイピング速度\(V^{\prime}\rm{[key/s]}\)の関係は,(2)式,(4)式より,
\[ V^{\prime} = \frac{x}{\it{T}_\rm{min} – \it{nT}_\rm{in} } \simeq \frac{x}{120 \it{-} \frac{\rm{(}\it{T}_{\rm{r}} + \it{T}_{\rm{j}} + \it{T}_{\rm{m}}\rm{)} \it{x}}{\rm{20}} } \rm{[key/s]}\cdots(5)\]
となります.ここで,上式を\(x\)について解き,
\[ x \simeq \frac{ 120V^{\prime} }{1 + \frac{(T_\rm{r} + \it{T}_\rm{j} + \it{T}_\rm{m} ) \it{V^{\prime}}}{20} }\cdots(6) \]
として(3)式に代入すれば(式が複雑なのであえて書きませんが),速度重視のタイピング速度\(V^{\prime}\)と正確性重視のタイピング速度\(V\)との比較,検討ができます.
また,実際にグラフを作ってみたので,それを下記に示します!
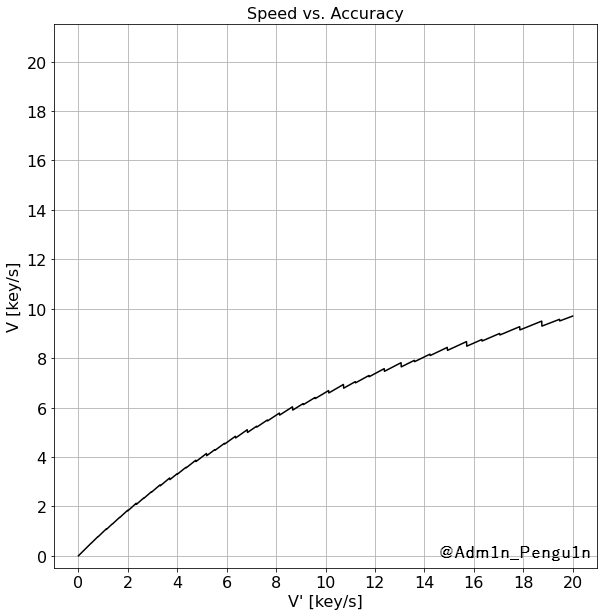
再び,この寿司打の動画から入力反応時間\(T_\rm{in}\)を20回計測して平均をとり,\(T_\rm{in} = \it{T}_{\rm{r}} + \it{T}_{\rm{j}} + \it{T}_{\rm{m}} = \rm{0.7941}… \simeq \rm{0.794} \)としました.
このグラフから読み取れることは,
- タイピング速度が速くなればなるほど,正確性重視の方がより優位になる傾向がある
- 特に,正確性重視の\(V=9\rm{key/s}\)は速度重視の\(V=18\rm{key/s}\)と同等以上の価値がある
他にも,当然ではありますが入力反応時間\(T_\rm{in}\)が短くなればなるほど,正確性重視の方がより優位になっていきます.
しかし,“タイピング速度”と“入力反応時間”はトレードオフの関係にあるため,その塩梅をどのようにするかは考察の余地があります.
正確性重視の場合はミスなしを前提としていますが,ミスする頻度を変化させて比較すると下図のようになります.
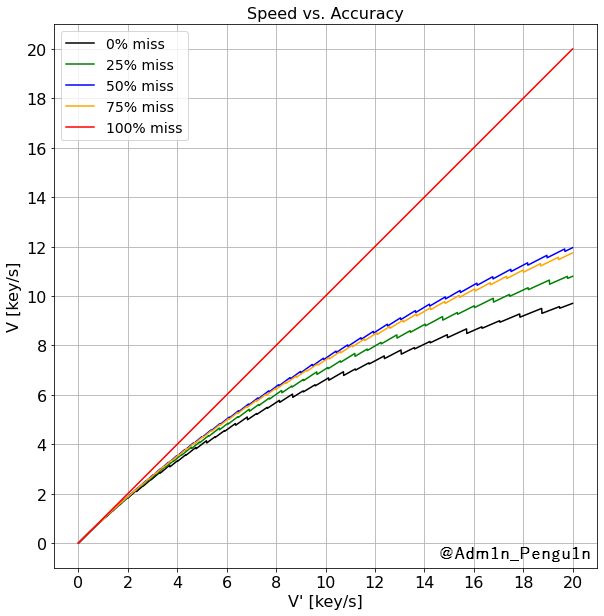
凡例の%の数値は,ミスした地点のゲーム画面上部のメーターの残りの長さの割合を示していて,それはミスの頻度とも言い換えられます.例えば,25% missならば合計4秒を追加されてすぐ誤打した場合となります.
あまり面白くない結果かもしれませんが,一応参考程度に載せておきました!

常にトップスピードでタイピングしようと意識するよりも、一段ギアを落として安定するスピードでタイピングした方が良さそうですね!
緊張について
何事でもそうですが,記録が出そうになると緊張するものです.
私はかなりの豆腐メンタルなので,特に記録が出そうになるとタイピング中に一種の邪念が脳内を駆け巡り,指の動きにかなりの影響が出ます(´;ω;`)
酷いときには,脳が考えることやめて一時停止してしまうんです!
タイピングの大会に出てる人は本当に本当に尊敬します!
ドナタカ,私ニ鋼ノメンタルヲクダサイ...

ボクもテストの前日はよく眠れないからわかるペン・・・!
おわりに
他の誰が書いた記事よりも詳しく,理論的に考察していきましたがいかがでしたか?
寿司打でスコアを上げるための最適解は,正確性重視のタイピング速度と速度重視のタイピング速度の比率によって,人それぞれ異なるということがわかったと思います!
検証してみた感想としては,体感していたよりも遥かに正確性を重視した方がスコアが伸びるということを知ることができ,スコアを上げるコツがわかったので満足です!
この研究を活かして,寿司打1位を目指して頑張っていきましょう!